Een aanneembare redenering.
Een redenering (gedachtegang, betoog) is het proces waarmee men op basis van een aantal argumenten,beweringen, premissen of axioma's tot een standpunt of conclusie komt. Een redenering is meestal deductief (het toepassen van een algemene regel op een specifieke situatie) ofinductief (het afleiden van een algemene regel uit een aantal specifieke situaties). Maar abductief redeneren (het zoeken van een zo goed mogelijke verklaring voor een aantal feiten) en analoog redeneren (van de ene specifieke situatie naar de andere specifieke situatie gaan en daar een waarschijnlijke conclusie uit trekken) bestaan ook. Een redenering is correct als het aan de voorwaarden geldigheid en gezondheid voldoet, anders is het eendrogreden. De vorm van een klassieke deductieve redenering is het syllogisme. Er zijn verschillende types redeneringen.Redenering
Deductie is een methode in de filosofie en in de logica, waarbij een gevolgtrekking wordt gemaakt uit het algemene naar het bijzondere - van de algemene regel (major-premisse) naar de bijzondere regel (minor-premisse) of waar de verzameling van premissen en de negatie van de conclusie inconsistent zijn.Deductie
[bewerken]Voorbeeld
| Major-premisse (algemene regel) | Alle mensen zijn sterfelijk. |
| Minor-premisse (bijzondere regel) | Socrates is een mens. |
| Conclusie | Socrates is sterfelijk. |
Een deductieve redenering van deze vorm noemt men ook een syllogisme. Deze redeneervorm is verder ontwikkeld en uitgebreid in diverse systemen van propositielogica en predicaatlogica, de meest gebruikte hiervan is de natuurlijke deductie. Tegenover deductie staat inductie, waarbij op grond van enkele bijzondere gevallen een algemene conclusie wordt getrokken.
[bewerken]Zie ook
Met inductie wordt, zowel in de huidige filosofische en wetenschappelijke betekenis, een manier vanredeneren bedoeld, die dient als bewijstechniek. Bij inductief redeneren komt men tot een algemene regel, generalisatie geheten, op grond van een aantal specifieke waarnemingen. In de logica wordt dit ook wel de ex consequentia-redenering genoemd. Hierbij probeert men tot een zo algemeen mogelijke regel te komen. Te denken valt aan wetten in juridische en natuurkundige zin en spraakkunstregels in de taalkunde. Een voorbeeld van inductie is de beroemde hypothese ‘alle zwanen zijn wit’. Deze conclusie komt voort uit een groot aantal waarnemingen van witte zwanen, zonder daarbij één enkele zwarte zwaan te observeren. De conclusies die volgen uit een inductieve redenering waarbij de vertrekpunten (premissen) waar zijn, kunnen waar maar ook onwaar zijn. In dit geval namelijk wanneer we één zwarte zwaan waarnemen. Deductie heet de tegenhanger van inductie. Daarbij gaat men van het algemene naar het bijzondere. Op logische wijze wordt dan de conclusie afgeleid uit de gegeven premissen. Uit de premissen ‘alle vogels zijn dieren’ en ‘alle zwanen zijn vogels’ kan worden geconcludeerd dat alle zwanen dieren zijn. Dit is een zogeheten syllogisme, waarin de modus tollens-redenering wordt gebruikt. Dit is een deductief argument: indien de premissen waar zijn, moeten de conclusies noodzakelijkerwijs ook waar zijn. Als men in dit geval de premissen verdedigt en de conclusie verwerpt, is er sprake van een contradictio in terminis ofwel een innerlijke tegenspraak.Inductie (filosofie)
Inhoud[verbergen] |
In de Oudgriekse filosofie speelde inductie ook een rol, met name bij Aristoteles (384 v.Chr. – 322 v.Chr.). Hierbij ging het echter niet om een soort redenering. Bij hem ging inductie niet alleen uit van zintuiglijkewaarnemingen, maar bleef ze er ook altijd aan gebonden. Wat mensen beweerden over hun ervaringen viel bij hem ook onder ‘verschijnselen’ (phainomena). Inzet van inductie was het verkrijgen van inzicht in een universeel zijnsaspect, waarbij intuïtief schouwen een belangrijke rol speelde. De aristotelische inductie had in feite niets van doen met statistiek, zoals bij de huidige inductie. Er is wel sprake van een serie waarnemingen, maar de laatste waarneming leidt dan tot het inzicht dat eerder nog niet tot de observator was doorgedrongen. Hier baseert de inductie zich dus op één geval. Dit betekent ook dat deze vorm van inductie niet propositioneel van aard was. Francis Bacon (1561-1626) legde al de nadruk op de inductieve methode. Later vierde het inductieprincipe hoogtijdagen ten tijde van het empirisme, met John Locke (1632-1704) als grondlegger. Deze stroming verdedigt de opvatting dat enkel de zintuiglijke waarneming als bron voor ware kennis kan gelden. Later vloeide het logisch positivisme hieruit voort, wat het handelsmerk van de Wiener Kreis was, dit betrof een groep wetenschappers en filosofen waaronder Moritz Schlick (1882-1936) en Rudolf Carnap (1891-1970). Logisch positivisten baseerden zich enkel op de waarneembare feiten, terwijl ze religieuze en metafysischeverklaringen resoluut van de hand wezen. Gedurende de eerste periode van wetenschap vormde het verhogen van de confirmatiegraad (de zekerheid vergroten door stijging van het aantal bevestigingen) hetdemarcatiecriterium (datgene wat wetenschap onderscheidt van niet-wetenschap), wat gebaseerd was op inductie. De spraakkunstregels van de klassieke talen Grieks en Latijn zijn vanzelfsprekend gebaseerd op inductieve waarnemingen, maar al vroeg is men tot vaststaande regels gekomen, waaraan men zich diende te houden om verzorgd taalgebruik te bereiken. Deductie als principe bij taalverwerving, of beter taalvervolmaking, had daardoor voorrang op inductie: men leerde de grammatica en de woordenlijsten, bestudeerde zgn.voorbeeldzinnen ofte lemmata (zinnen die men vond bij de erkende klassieke auteurs) en stelde zo correcte zinnen op in het Grieks, Latijn en later in alle westerse talen. Pakweg einde de jaren 60 van de 20e eeuw werd er in het vreemde talenonderwijs veel meer plaats ingeruimd voor een wijze van inductieve taalverwerving: men confronteerde de student alleen nog maar met tekst en voegde, indien nodig of indien er vraag naar bleek, grammaticale richtlijnen toe. Degenen die altijd hadden gepleit voor de aloude deductieve methode vonden en vinden dat met de inductieve methode geen inzicht in de structuur van een taal kan worden verworven. De inductieve methode heeft nochtans de deductieve methode in het taalonderwijs verdrongen en daar zijn verklaringen voor: er is niet altijd tijd voor de studie van een taalstructuur; de noodzaak en het nut van het kennen van enkele woorden en zinnetjes die men begrijpt binnen een specifieke context en de `slordige vlotheid´ waarmee men die kennis verwerft, kunnen primordiaal zijn (oorlog, toerisme). Bedenk dat militaire (taal)dril allereerst met een inductieve aanpak verwant is: bij de bevrijding van Europa en Azië tussen 1942 en 1945 moesten Amerikanen, Engelsen en alle meevechtende kolonialen zo snel mogelijk via herhaling en geheugenoefeningen een mondje Duits, Japans, Frans, Italiaans en Spaans verwerven, meestal op het niveau van kindertaal. Spraakkunst, die men per definitie trager verwerft (weliswaar ook met een zekere dril), is in zulke utilitaire omstandigheden een verwaarloosbare zorg. In het dagelijks leven maken we voortdurend gebruik van inductieve argumenten. Bij een heleboel zaken verwachten we dat de toekomst op het verleden zal lijken. Bijvoorbeeld dat eten ons zal voeden, dat drinken onze dorst zal lessen, dat de nacht zal volgen op de dag, dat we nat worden als we buiten in de regen staan, dat de grond niet onder onze voeten zal wegzakken wanneer we er overheen lopen enzovoorts. We koesteren vertrouwen in de regelmaat van de werking der natuur. De eerste die een probleem schetste bij inductie was de Schotse filosoof David Hume (1711-1776). Hij gaf aan dat het de mens niet was gegeven een oneindig aantal gevallen waar te nemen, er is steeds sprake van een eindig aantal waarnemingen. Derhalve is het onmogelijk voor de mens om universele uitspraken te rechtvaardigen aangaande dewerkelijkheid op basis van ervaring. Bovendien betoogde hij dat we nooit zekerheid hebben over hoe de toekomst eruit zal zien op basis van het verleden. De conclusie die kan worden getrokken uit Hume’s kritiek op inductie is dat ze geen absolute, universele geldigheid met zich brengt, in tegenstelling tot conclusies uit deductieve argumenten. Het probleem van de inductie betekent in feite de vraag hoe we ooit kunnen rechtvaardigen dat we blijven redeneren op zo’n manier. Een ander kritiekpunt op inductie werd ontwikkeld door de Amerikaanse filosoof Nelson Goodman(1906-1998). Hierbij gaat het om het idee dat er bij inductief redeneren meerdere conclusies kunnen worden getrokken op basis van het beschikbare bewijsmateriaal. Dit leidt er vervolgens toe dat er verschillende voorspellingen voor de toekomst zullen worden gedaan. Het gedachte-experiment waarmee hij dit wilde aantonen staat bekend als de ‘grue-paradox’. ‘Grue’ is een kunstmatige kleuraanduiding. Iets is ‘grue’ als het is bekeken vóór het jaar x en toen groen (green) bleek te zijn, of als het niet is bekeken en blauw (blue) is. Op grond van heel wat waarnemingen kan de generalisatie worden verdedigd dat alle smaragden groen zijn. Maar het bewijsmateriaal voldoet in gelijke mate aan de hypothese dat alle smaragden ‘grue’ zijn (mits alle waarnemingen voor het tijdstip x hebben plaatsgevonden). Maar deze twee verschillende conclusies zijn van invloed op de voorspellingen die kunnen worden gedaan over waarnemingen na het tijdstip x. Als wordt beweerd dat alle smaragden ‘grue’ zijn, wordt daarmee voorspeld dat sommige smaragden die na tijdstip x worden waargenomen blauw zullen ogen. Toch is het veel waarschijnlijker dat alle smaragden groen zijn, maar dan wordt voorspeld dat ze allemaal groen zullen ogen wanneer ze worden bekeken. Nog een ander probleem bij inductie betreft de zogeheten ravenparadox van de Duitse logicus Hempel. Zie hiervoor de paradox van Hempel. Er is een aantal pogingen ondernomen om het inductieprobleem op te lossen. Denkers als Braithwaite en Black waren van mening dat inductie is gerechtvaardigd, aangezien het altijd heeft gewerkt. Het is een nuttige methode gebleken om regelmatigheden in de natuur te ontdekken en voorspellingen over het toekomstig gedrag van natuurverschijnselen te doen. Het kritiekpunt hierop is dat er sprake is van eencirkelredenering. Het inductieprincipe wordt zelf namelijk verdedigd met een inductief argument. Inductie zou dan in de toekomst werken aangezien dit in het verleden tevens het geval was. Ook deze generalisatie is gebaseerd op een aantal specifieke voorbeelden van de werking van inductie. Men heeft ook wel geprobeerd het inductieprobleem op te lossen aan de hand van inductieve logica. Bij inductieve logica wordt een poging ondernomen een gerechtvaardigde ‘sprong’ naar de generalisatie te maken, door de conclusie uit gegeven premissen tot een bepaalde hoogte te confirmeren. Het is hierbij niet zo dat de premissen de conclusie impliceren. De problemen hierbij zijn in feite hiervoor al geschetst, namelijk de grue- en ravenparadox. Deze twee gedachte-experimenten illustreren dat inductieve logica in tegenspraak is met de menselijke intuïtie. Een andere manier waarmee men het inductieprobleem te lijf is gegaan vormt de waarschijnlijkheidsoplossing. Van de natuurwetten die door de wetenschap zijn ontdekt, is niet bewezen dat ze absoluut geldig zijn, het zijn generalisaties waarvan het hoogst waarschijnlijk is dat ze waar zijn. Hoe vaker een hypothese wordt bevestigd, des te waarschijnlijker is het dat ze waar is. Dit noemt men hetprobabilisme. Het probleem hierbij is nu dat waarschijnlijkheid zou kunnen veranderen in de toekomst. Het bepalen van de mate van waarschijnlijkheid in de toekomst wordt gebaseerd op de frequentie waarmee het in het verleden heeft plaatsgehad. De enige rechtvaardiging voor deze veronderstelling is van zichzelf inductief, waarmee er weer sprake is van een cirkelredenering. Daarnaast blijft bij deze theorie de vraag open wat nu wel en niet precies onder waarschijnlijkheid moet worden verstaan, plus het feit dat er altijd een selectie dient plaats te vinden bij een onderzoek, wat altijd een extra aanname met zich meebrengt aangaande juiste representatie. Het Bayesianisme is een leer die uitgaat van de waarschijnlijkheidstheorie. Vervolgens bestaat er een benaderingswijze die uitgaat van evolutie. De grue-paradox van Goodman laat zien dat er niet één enkele manier bestaat waarop we eigenschappen kunnen toekennen aan waargenomen objecten. Tegelijkertijd laat dat voorbeeld zien dat sommige generalisaties duidelijk aannemelijker zijn dan andere. Een mogelijke verklaring hiervoor kunnen we vinden door naar onze evolutie te kijken. Mensen worden geboren met een genetisch geprogrammeerde groep categorieën die als het ware worden losgelaten op onze zintuiglijke indrukken. Deze categorieën zijn nodig voor de verwerkelijking van onze aanschouwingen. Plato (427 v.Chr. - 347 v.Chr.)was de eerste denker die betoogde dat onze ziel over aangeboren ideeën beschikt, wat later door de rationalisten werd uitgelegd in termen van a priori-principes van het verstand die zelfstandig kennis konden aanmaken. Immanuel Kant (1724-1804) was degene die twaalf a priori-principes van het verstand formuleerde in zijn "Kritik der reinen Vernunft". Hij kwam met de volgende indeling: er zijn categorieën van kwantiteit (eenheid, veelheid en totaliteit), van kwaliteit (negatie, bevestiging en uitsluiting) van relatie (substantie-accident, oorzaak-gevolg en wisselwerking) en van modaliteit (mogelijkheid-onmogelijkheid, werkelijkheid-onwerkelijkheid en noodzakelijkheid). Deze categorieën hebben we verkregen middels een proces van natuurlijke selectie. Dankzij deze categorieën hebben we geneigdheden verworven om inductieve generalisaties over de werking van de natuur redelijk nauwkeurig te voorspellen. Dit wil niet zeggen dat ons vertrouwen op inductie is gerechtvaardigd, maar het biedt een verklaring waarom we vertrouwen koesteren in inductieve argumenten. De meest succesvolle methode om inductie het hoofd te bieden binnen de wetenschap bood deOostenrijkste wetenschapsfilosoof Karl Popper (1902-1994). Zijn falsificatietheorie gaat uit van het idee dat inductie helemaal niet de basis vormt van de wetenschappelijke werkwijze. Wetenschappelijke theorieën hebben volgens hem geen waarheidspretentie. We moeten ze beschouwen als voorlopig, en dienen juist proberen te bewijzen dat ze onjuist zijn. Zo wordt wetenschap een proces van gissing en weerlegging. Haar vooruitgang schuilt hierin, dat theorieën in de loop van de tijd worden vervangen door betere theorieën, die de waarheid steeds dichter benaderen. De logische kracht van één falsificatie is sterker dan een oneindig aantal verificaties van een hypothese. Bijgevolg was volgens Popper het verhogen van de falsificatiegraad het nieuwe demarcatiecriterium voor de wetenschap. Theorieën die niet kunnen worden weerlegd waren in zijn ogen dan ook onwetenschappelijk, zoals de psychoanalyse van Freud (1856-1939). De wetenschapsfilosofische moeilijkheid die hierbij optreedt is in het kader van inductie dat er geen rationelebasis meer bestaat om voorspellingen van een theorie te geloven. Een definitieve scheiding tussen verificatie en falsificatie lijkt niet mogelijk, aangezien de weerlegging van de theorie dat alle A’s eigenschap B bezitten de hypothese bevestigt dat sommige A’s de eigenschap B bezitten. Popper introduceerde de termen empirische inhoud en corroboratiegraad, teneinde een keuze te kunnen maken tussen twee elkaar beconcurrerende theorieën die beide niet gefalsifieerd zijn. Met de empirische inhoud wordt de mate van informatie die een theorie levert bedoeld. Hoe meer er door een theorie wordt voorspeld, hoe beter. Met de corroboratiegraad wordt de zwaarte van de toetsing bedoeld. Wanneer er een keuze wordt gemaakt tussen twee theorieën op basis van deze twee principes, betekent het toch dat het idee van bevestiging een rol speelt. In feite krijgt inductie ook geen plaats in het wetenschapsdenken van de Amerikaanse filosoof Thomas Kuhn(1922-1996). Bij hem introduceren we ook een nieuwe theorie wanneer zijn voorganger is gefalsifieerd. Dit gebeurt volgens hem echter niet op basis van logica en rationaliteit. Hij plaats daarentegen wetenschap in een sociologische en sociaal-psychologische context, en ontkent dat er binnen de wetenschap sprake is van vooruitgang. Hij spreekt van paradigma’s, dit zijn raamwerken waarbinnen wetenschap wordt bedreven, en waarin duidelijkheid bestaat over de concepten, methoden en toepassingen die gelden voor een bepaalde periode en een bepaald wetenschapsdomein. Gedurende de periode van ‘normale wetenschap’ kan het betreffende paradigma alle problemen met succes te lijf gaan. Het paradigma kan in een crisis terechtkomen wanneer ze problemen niet meer kan oplossen, zodat er een wetenschappelijke revolutie uitbreekt. Dit betekent een strijd tussen twee groepen, zeg maar de ‘normalen’ en ‘revolutionairen’, die zal resulteren in een nieuw paradigma. Het idee van bevestiging speelt bij Kuhn dus wel een rol waar het gaat om een paradigma als geheel. De wetenschapsfilosofie van de Hongaarse filosoof Imre Lakatos (1922-1974) kan worden beschouwd als een synthese tussen het denken van Popper en Kuhn, en wordt wel het verfijnd falsificationisme genoemd. Hij houdt vast aan het idee van vooruitgang en rationaliteit in de wetenschap, maar gaat tevens uit van de gedachte dat een theorie altijd ligt verankerd in een onderzoeksprogramma (wat Kuhn een paradigma noemt). In een onderzoeksprogramma lossen theorieën elkaar af, terwijl ze allemaal beschikken over een harde kern. De harde kern is datgene waaraan in theorieën niet kan worden getornd. Een onderzoeksprogramma wordt geleid door twee methodologische regels, de zogeheten negatieve en positieve heuristiek. De negatieve heuristiek beschermt de harde kern van het programma, de positieve heuristiek bepaalt welke aspecten van een theorie ter discussie mogen worden gesteld. Inductie neemt bij Lakatos een meer centrale plaats in dan bij Popper en Kuhn. Verificatie van een gedurfde theorie zou naar zijn zeggen vooruitgang met zich mee kunnen brengen, terwijl het falsificatieprincipe het beste past bij voorzichtige theorieën. De opvolging van een oude theorie door een nieuwe is dus afhankelijk van de positieve heuristiek. Het standaardbeeld van de wetenschap bestaat uit drie elementen: Ad. 1. is een methode van wetenschappelijk onderzoek die bestaat uit een herhalende cyclus van hypothesenvorming, deductie van voorspellingen uit deze hypothesen, de empirische toetsing van deze voorspellingen en waar mogelijk de herziening van de hypothesen. De meest gevolgde procedure om tegenwoordig tot wetenschappelijke kennis te komen is de zogeheten empirische cyclus. Zie hiervoor de wetenschappelijke methode. In deze cyclus komt het principe van inductie in meer of mindere mate voor. Wanneer er op basis van een bepaald aantal waarnemingen een theorie/hypothese wordt gevormd, is dit op basis van inductie. Aan de hand van deductief redeneren kan men vervolgens tot een voorspelling komen. Door het uitvoeren van experimenten wordt deze voorspelling getoetst. De resultaten die uit de bus komen moeten worden geëvalueerd, dit kan middels hetverificatieprincipe (inductie) en het falsificatieprincipe(deductie).
[bewerken]Inductie in de Griekse filosofie
[bewerken]Inductieve wetenschap
[bewerken]Inductie in de taalverwerving
[bewerken]Het probleem van de inductie
[bewerken]Oplossingen voor het inductieprobleem
[bewerken]De rol van inductie in de wetenschap
[bewerken]Inductie binnen de huidige wetenschappelijke methoden
Ad. 2. Bestaat uit 5 fasen: observatie, inductie, deductie, toetsing en evaluatie.
Ad. 3. De kern van het verklaringsmodel bestaat uit twee principes: de symmetrie-these en de covering-law-these.
[bewerken]Zie ook
Abductie is een redeneervorm, waarbij een verklaring wordt geselecteerd op grond van waarschijnlijkheid. In een abductieve redenering wordt aangenomen dat de meest waarschijnlijke conclusie de juiste is. In het Engels wordt deze redeneervorm derhalve vaak inference to the best explanation (IBE) genoemd. Deze redeneervorm wordt soms gebruikt in onderzoek, waarbij men niet met zekerheid (deductief) de conclusie kan afleiden. Als zodanig is deze redeneervorm verwant aan inductie. De getrokken conclusie is weliswaar waarschijnlijk, maar niet zeker en mogelijkerwijs onwaar.Abductie (filosofie)
[bewerken]Voorbeeld

In de logica is een analogiebewijs een redeneervorm waarbij men op grond van een vergelijking met een ander geval een conclusie afleidt.Analogiebewijs
Inhoud[verbergen] |
In standaard predicatenlogica kan een analogie als volgt worden geconstrueerd: Er kan worden onderscheiden tussen een sterke analogie en een zwakke analogie. Bij een zwakke analogie zijn de eigenschappen van de vergeleken objecten niet volledig identiek. Zwakke analogieën zijn minder overtuigend, omdat de conclusie niet noodzakelijk is. Een voorbeeld: Anders gezegd: "Jan heeft kanker, Piet heeft kanker en Jan overlijdt aan (zijn) kanker. Hieruit concludeert men dat Piet zal overlijden." Dit is een voorbeeld van een zwakke analogie aangezien de eigenschappen van Jan en Piet niet identiek zijn (verschillend DNA, verschillende levensomstandigheden, etc..). Het hoeft dus niet zo te zijn dat Piet zal overlijden aan zijn kanker.
[bewerken]Formele notatie
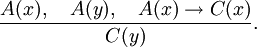
[bewerken]Typen
[bewerken]Voorbeeld

[bewerken]Externe links
Een geldige redenering is in de logica en argumentatieleer een redenering die qua vorm voldoet aan de voorwaarden van een goede deductieve redenering. Dat wil zeggen dat de conclusie noodzakelijk volgt uit de premissen. Het is niet noodzakelijk voor een geldige redenering dat de premissen an sich waar zijn: als de vorm van de redenering zelf maar klopt. Een redenering die én geldig is én waarvan de premissen evident waar zijn noemt men valide. Deze redenering is geldig omdat, als je de premissen A en B voor waar aanneemt, de conclusie C noodzakelijk volgt. Zij is echter niet valide omdat de premisse B niet evident waar is. Deze redenering is zowel geldig als valide.Geldigheid en gezondheid
Een syllogisme is in de logica een redenering, die bestaat uit drie proposities: een majorpremisse, een minorpremisse en een conclusie. De proposities bevatten een minor term of subject, een major term ofpredicaat en een middenterm. In syllogismen komen vier soorten proposities voor: Er zijn vier verschillende geldige syllogismen: Barbara, Celarent, Darii en Ferio. Een redenering op basis van deze syllogismen heet categorische deductie. Een bekend voorbeeld van een syllogisme is de volgende geldige redenering: Dit syllogisme is een geldige redenering, omdat de conclusie noodzakelijkerwijs voortvloeit uit de voorafgaande premissen. De majorpremisse is universeel bevestigend en de minorpremisse en conclusie zijn particulier bevestigend. Socrates is de minorterm, mens is de middenterm en sterfelijk is het predicaat. De conclusie is waar omdat de voorafgaande premissen ware beweringen zijn. In de retorica van Aristoteles is een enthymeem een retorisch syllogisme. Deze redenering is formeel geldig, want de conclusie vloeit noodzakelijk voort uit de twee premissen. Maar de conclusie is niet waar, omdat de bewering in de eerste premisse niet waar is. Een ander fout voorbeeld : Deze redenering is formeel ongeldig, want de conclusie wordt impliciet getrokken uit "Alle auto's die voor 1994 zijn gebouwd hebben geen katalysator", maar dit is geen geldige inversie van de majorpremisse, want er kunnen wel degelijk auto's van voor 1994 zijn die wel een katalysator hebben. Tot in de negentiende eeuw was de Aristotelische logica, waar de syllogistiek de technische inhoud van vormt, het enige gehanteerde systeem. Sindsdien heeft Boole de propositielogica en later (1879) Frege depredicatenlogica ontwikkeld. De propositielogica heeft taalkundig een andere benadering dan de syllogistiek: zij kent geen predicaten, maar wel connectieven. Zowel de syllogistiek als de propositielogica zijn te interpreteren binnen de predicatenlogica.Syllogisme
[bewerken]Voorbeelden
[bewerken]Plaats van de syllogistiek in de logica